Test of hypothesis about the population mean

When the population standard deviation (S) is identified then the t statistic is defined as

            t = ¦(x¯ - µ)/ S_x¯¦        whereas: S_x¯ = s/√n

Follows the students t distribution along with (n-1) d.f. whereas

      x¯ = Sample mean

      μ = Hypothesis population mean

      n = sample size

And S is the standard deviation of the sample calculated though the formula

S=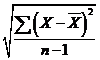

for n < 30

If the calculated value of t exceeds the table value of t at a particular level of significance, the null hypothesis is rejected.

Illustration

Ten oil tins are taken at random from an automatic filling machine. The mean weight of the tins is 15.8 kilogram (kg) and the standard deviation is 0.5 kilogram (kg). Does the sample mean differ significantly from the intended weight of 16 kilogram (kg). Use 5 percent level of significance.

Solution

Described that n = 10;   x¯= 15.8; S = 0.50; μ = 16; v = 9

      H₀: μ = 16

      H₁: μ ≠ 16

            = 

t = ¦ {(15.8 - 16)/(0.5/√10)}¦

      = ¦{0.2/0.16}¦

      = -1.25

The table value for t for 9 d.f. at 5 percent level of significance is 2.26. The computed value of t is smaller than the table value of t. hence, difference is insignificant and the null hypothesis is accepted.