In this section we will take a look at something that we utilized back while we where graphing parabolas.  Though, we're going to take a more common view of it this section. Several graphs have symmetry to them.

In graphing Symmetry can be useful an equation as it says that if we know one portion of the graph then we will also know the left over (and symmetric) portion of the graph as well. We utilized this fact while we were graphing parabolas to obatin an extra point of some of the graphs.

In this section we desire to look at three types of symmetry.

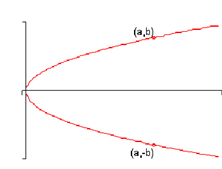
1.   A graph is said to be symmetric around the x-axis if whenever ( a, b) is on the graph then hence is ( a, -b ) .  Following is a sketch of a graph which is symmetric around the x-axis.

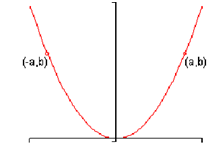
1.      A graph is said to be symmetric around the y-axis if whenever ( a, b) is on the graph then hence is ( -a, b ) .  Following is a sketch of a graph which is symmetric around the y-axis.

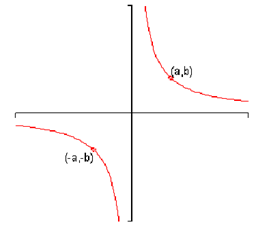
3.   A graph is said to be symmetric around the origin if whenever ( a, b ) is on the graph then hence is ( -a, -b ) .  Following is a sketch of a graph which is symmetric around the origin.

Note that most of the graphs don't have any sort of symmetry.  Also, it is possible for a graph to have more than one type of symmetry. For instance the graph of a circle centered at the origin exhibits all three kinds of symmetries.