States of stress - principal stresses:

Now let us consider a few cases of solids of the similar material (mild steel) under various states of stress as display in Figure. The given states of stress have already been decreased within terms of principal stresses. Poisson's ratio v is given as 0.3.

Solution

Case a

First, let us consider the solid shown in Figure (a).

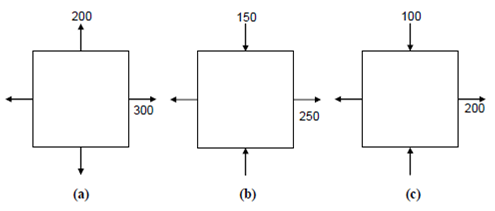
Figure

(a)        Since the major principal stress, σ1 (300 MPa) is more than

σy (260 MPa), the solid will fail according to principal stress theory.

(b)        The maximum principal strain, ε1 = 300/E -0.3 (+200)/E

=240/E < 260/E

∴          According to principal strain theory, the solid is safe.

(c)        Maximum shear stress, τ_max  =300-200/2 = 50<<130

∴          The solid is safe according to shear stress theory too.

(d)        Total strain energy density in the solid, u is as follows:

 u = 1/2E [300² +200² -2 ×0.3×300×200] = 47000/E > 260²/2E

∴          The solid will fail according to total strain energy theory.

(e)        Distortion energy density in the solid, u_d as follows:

u_d = 1/12G [(300-200)² + 200² + 300²] = 70000/6G > 260²/6G

∴          Distortion energy theory also predicts that the solid will fail.