Solve each of the following.

                             |x - 2 | = 3x + 1

Solution

At first glance the formula we utilized above will do us no good here.  It needs the right side of the equation to be a +ve number.  It turns out that still we can use it here, however we're going to have to be careful along the answers as using this formula will, on instance introduce an incorrect answer. Thus, whereas we can use the formula we'll have to make sure we check our solutions to see if they work really.

                                                    |x - 2| = 3x + 1

Thus, we'll start off using the formula above as we have in the earlier problems and solving the two linear equations.

x - 2 = - (3x + 1) = -3x -1    or            x - 2 = 3x + 1

4x = 1  or                                 - 2x = 3

x =1/4                              or     x = - 3/2

Okay, here we've got two potential answers. However there is a problem along with the second one.  If we plug this one into the equation we get,

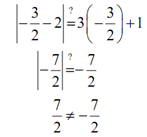                                          NOT OK

We get the similar number on each side however with opposite signs. It will happen on occasion while we solve this kind of equation with absolute values.  Note that we actually didn't have to plug the solution in the whole equation here.  All we required to do was check the portion without the absolute value & if it was -ve then the potential solution will not actually be a solution and if it's positive or zero it will be solution.

Now ,You should yourself verify that the first potential solution does in fact work and so there is single solution to this equation: x =1/4 and notice that this is less than 2 (as our supposition needed) and thus is a solution to the equation with the absolute value in it.

Thus, all together there is a single solution to this equation: x = ¼.