Estimation of population mean

If the sample size is small (n<30) the arithmetic mean of small samples are not normally distributed. In such conditions, student's t distribution must be utilized to estimate the population mean.

In this case

Population mean µ = x¯ ±  tS_x¯

 x¯ = Sample mean

S_x¯ =  s/√n

S = standard deviation of samples =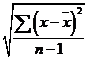

for small samples.

n = sample size

v = n - 1 degrees of freedom.

The value of t is acquired from student's t distribution tables for the essential confidence level

Illustration

A random sample of 12 items is taken and is found to have a mean weight of 50 gram and a standard deviation of 9 gram

What is the mean weight of population

a)         Along with 95 percent confidence

b)         Along with 99 percent confidence

Solution

   S = 9; v = n - 1 = 12 - 1 = 11;          

S_x¯ = s/√n = 9/√12        

µ = x¯ ± t S_x¯ 

At 95 percent confidence level

µ = 50 ± 2.262

= 50 ± 5.72 grams

Hence we can state with 95 percent confidence that the population mean is among 44.28 and 55.72 gram

At 99 percent confidence level

µ = 50 ± 3.25 (9/√12)

= 50 ± 8.07 gram

 Therefore we can state with 99 percent confidence that the population mean is between 41.93 and 58.07 grams

Note: To employ the t distribution tables it is significant to find the degrees of freedom (v = n - 1). In the illustration above v = 12 - 1 = 11

From the tables we find that at 95 percent confidence level against 11 and under 0.05, the value of t = 2.201