Example Sketch the graph of following
f( x ) = 2x and g( x ) = ( 1 /2)x
Solution
Let's firstly make a table of values for these two functions.
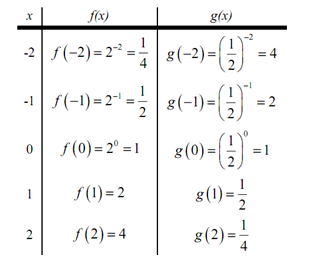
Following is the sketch of both of these functions.
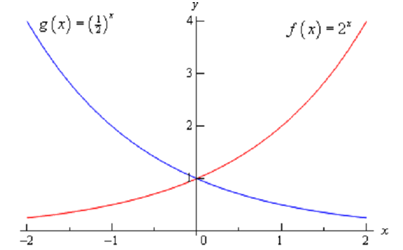
This graph shows some very nice properties regarding exponential functions in general.
Properties of f( x ) = b x
1. f(0)= 1. The function will take the value of 1 at x=0 always
2. f( x ) ≠ 0 . An exponential function will never get zero.
3. f( x ) > 0 . An exponential function is always get positive.
4. The previous two properties can be summarized through saying that the range of an exponential function is (0, ∞ ) .
5. The domain of exponential function is [ -∞, ∞ ] . In other terms, you can plug every x in an exponential function.
6. If 0 < b < 1 then,
a. f ( x ) → 0 as x → ∞
b. f ( x ) → ∞ as x → -∞
7. If b >1 then,
a. f (x ) → ∞ as x → ∞
b. f ( x ) → 0 as x → -∞
These will all be extremely useful properties to remember .