Simulation of a pn Junction

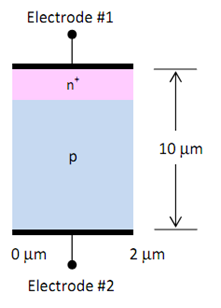
An n⁺ p junction is fabricated on a p-type silicon substrate with N_A = 8×10¹⁵ cm^-3 . The n+ region has a concentration of N_D = 1.5×10¹⁸ cm^-3 and a junction depth of x_j = 1.4 μm. The total device depth is 10 μm (from top to bottom contact).

Use Sentaurus to simulate and view the results for the following conditions:

1. Zero Bias, Uniform Doping Profiles Using uniform doping profiles, verifies the 1D and 2D doping concentration of this junction. Also plot the 1D potential across the junction to estimate the built-in potential and depletion region width. Compare the results with the theoretical values.

You may want to use a non-uniform mesh, which is denser in the top 2 μm of the device.

2. Reverse Bias, Uniform Doping Profiles Simulate the diode under reverse bias. Plot the reverse IV characteristics and extract the breakdown voltage. Compare your result with Figure in the text. What is the maximum electric field in the junction just before breakdown?

3. Forward Bias, Uniform Doping Profiles Plot the IV relation for this diode under a forward bias between 0 and 1 V. What allows us to raise the forward bias above 0.7 V? How can this be seen from the simulation output?

Hint: Examine the change in the IV curve with increasing voltage and determine the cause of this change.

4. High Temperature, Uniform Doping Profiles The junction temperature is raised to 580°C. Simulate this junction up to a reverse bias of 12V and a forward bias of 1V. Plot and explain the IV characteristics.

5. Reverse Bias, Gaussian n+ Doping Profiles Using a Gaussian profile for the n⁺ region with peak concentration of 1.5×10¹⁸ cm^-3 and junction depth of x_j = 0.7 μm, verify the 1D and 2D doping concentration of the junction. Plot the 1D potential across the junction to estimate the built-in voltage and depletion width at equilibrium. Compare V_bi with the theoretical value and compare V_bi and junction width to those from part 2. Also, estimate the minority carrier diffusion lengths L_n and L_p.