Resultant of Concurrent Force System:
The resolution of forces helps in finding out the resultant of a number of forces working on a body as it decrease vectorial addition to algebraic addition.
If more than two coplanar, concurrent forces are working on a body, the analytical method of seeking resultant is quicker. Each of the force is resolved out into two mutually perpendicular axes say x and y. All of the components along with the respective axes are added algebraically to obtain the components of the resultant R along x and y axes. Therefore, we obtain
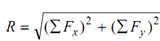
tan θx = ∑ Fy / ∑ Fx
where, θx = angle which the resultant R makes with the x-axis.
In particular case of non-coplanar forces, the given force is resolved out into three mutually perpendicular axes system, for example. x, y and z axes. Therefore, we obtain
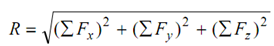
cos θx = ∑ Fx / R, cos θ y =∑ Fy / R, cos θz = ∑ Fz/ R
where ∑ Fx , ∑ Fy and ∑ Fz are the algebraic sums of the components of all of the forces along with x, y and z axes, respectively. The angles θx, θy and θz are the angles which the resultant R makes along with x, y and z axes, respectively.
The measure of the property of a force through virtue of which it tends to rotate the body on which it behaves is called the moment of a force.
A couple is a force system contains two equal, coplanar, parallel forces working in opposite direction.