Prove that the ratio of belt tension is given by the T1/T2  = e^μθ

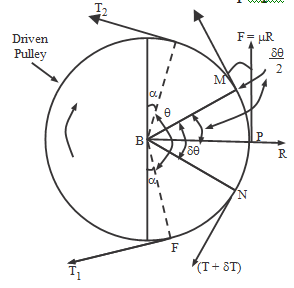
Let  T1 = Tension in belt on the tight side T2 = Tension in belt on the slack side θ = Angle of contact

μ = Co efficient of friction existing between belt and pulley.

α = Angle of Lap

Consider driven or follower pulley. Belt remains in contact with the EBF. Let T₁ and T₂ are the tensions in tight side and slack side.

Angle EBF known as angle of contact = ∏.-2α

Consider driven or follower pulley.

Belt remains in contact with the NPM. Let T1  and T2  are tensions in tight side and slack side. Let T be tension at point M & (T + dT) be the tension at point N.

Consider equilibrium in horizontal Reaction 'R' and vertical reaction µR.

Since the whole system is in equilibrium, that is

ΣV = 0; Tsin (90 - δq/2) + µR - (T + δT)sin(90 - δθ/2) = 0

Tcos (δθ/2) + µR = (T + δT) cos (δθ/2)

Tcos (δθ/2) + µR = Tcos(δq/2) + δTcos(δθ/2)

µR = δTcos(δθ/2)

Since δθ/2 is very small and cos0° = 1, So cos(δθ/2) = 1

µR = δT                                                                                                                                   ...(i)

ΣH = 0;

R-Tcos(90 - δq/2)-(T + δT)cos(90 - δθ/2) = 0

R = Tsin(δθ/2) + (T + δT)sin(δθ/2) As δθ/2 is small So sin(δθ/2) = δθ/2

R = T(δθ/2) + T(δθ/2) + δT(δθ/2) R = T.δθ + δT(δθ/2)

As δT(δq/2) is very small  So δT(δq/2) = 0

R = T.δq                                                                                                                               ...(ii)

Putting value of (ii) in equation (i)

µ.T.δθ = δT

or,                    δT/T = µ.δθ

Integrating both theside: 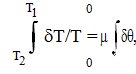, Where θ = Total angle of contact

ln(T₁/T₂) = µ.θ

or,                   T₁/T₂ = e^µ.θ

Ratio of belt tension = T₁/T₂  = e^µθ

Belt ratio is represent as 2.3log(T₁/T₂) = µ.q

Note that θ is in radian

In this formula the important thing is Angle of contact(θ)