Phong Specular Reflection Model or Specular Reflection

This model of local illumination is frequently termed as the Phong specular reflection model. Here we discuss the matter of specular reflection in a more practical manner. See the figure 9 where if R is the ways of specular reflection and V is the ways of the viewer as assigned at the View Reference Point or VRP, then for a perfect reflector the specular reflection is visible merely while V and R coincide. For actual objects as not ideal reflectors the specular reflectance can be seen even if V and R don't coincide, that is observable over range of values or a cone of values. The shinier the surface, the minor the f(α) range for specular visibility. Thus a specular reflectance model should have maximum intensity at R, along with an intensity that decreases like f (α).

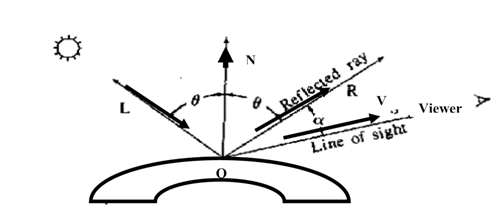
From the above discussion we found that Specular reflection is the consequence of total or near whole reflection of the light in a concentrated region near the specular reflection angle as a and the description of other variables demonstrated in the figure 8 as:

Note:

N        → Unit normal surface vector

R         → Unit vector in the direction of ideal specular reflection

L         → Unit vector in the direction of pt. Light source

V         → Unit vector pointing the viewer.

a          → viewing angle relative to R .

- At a = 0 viewer will observe light of more intensity.

- In case of perfect reflection or ideal mirror, incident light is reflected merely in specular reflection direction.

- Objects the other than perfect reflection exhibit specular reflection over a finite range of viewing positions nearby R as shiny surfaces have narrow specular reflection range and dull surfaces have broad range.