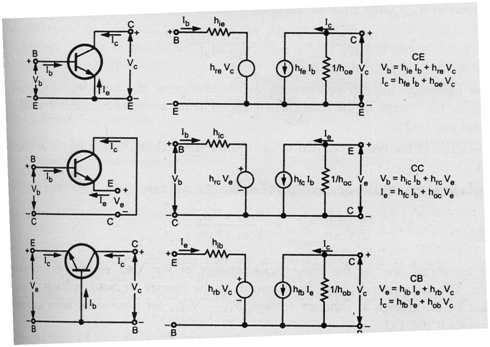
Partial derivatives - Transistor hybrid model:

The partial derivatives are taken by keeping the collector voltage or base current constant as pointed out by the subscript attached to the derivative.

Δv_B , Δv_C ,  Δ i_C , Δ i_B present the small signal(increment) base and collector voltages and currents, they are presented by symbols   v_b , v_c , i_b and  i_c correspondingly. 

 Eqs (3) and (4) may be written like as follow:

             V_b = h_ie i_b + h_re V_c                                                                 

              i_c = h_fe i_b + h_oe V_c

in which   h_ie =(∂f₁/∂i_B)V_c =  (∂v_B/∂i_B)V_c = (Δv_B /Δi_B)V_c = (v_b / i_b)V_c         

                  h_re =(∂f₁/∂v_c)I_B   =  (∂v_B/∂v_c) I_B = (Δv_B /Δv_c) I_B = (v_b /v_c) I_B

                h_fe  =(∂f₂/∂i_B)V_c =  (∂i_c /∂i_B)V_c = (Δ i_c /Δi_B)V_c = (i_c / i_b)V_c

                h_oe= (∂f₂/∂v_c)I_B   =  (∂i_c /∂v_c) I_B = (Δ i_c /Δv_c) I_B = (i_c /v_c) I_B

The above equations described the h-parameters of the transistor in CE configuration. Similar theory can be extended to transistors in additional configurations.

Hybrid Model and Equations for the transistor in three dissimilar configurations are displayed below.