Let us firstly illustrate the idea of merging two sorted sequences using a odd-even merging circuit. The functioning of a merging circuit is as follows:

1)   Let there be two sorted series A=(a1, a2, a3, a4......... am) and B=(b1, b2, b3, b4......... bm) which are required to be merged.

2)   With the help of a merging circuit (m/2, m/2), merge the odd indexed numbers of the two sub series i.e. (a1, a3, a5......... am-1) and (b1, b3, b5......... bm-1) and thus resulting in sorted series (c1, c2, c3......... cm).

3)   After that, with the help of a merging circuit (m/2,m/2), merge the even indexed numbers of the two sub series i.e. (a2, a4, a6......... am) and (b2, b4, b6......... bm) and therefore resulting in sorted series (d1, d2, d3......... dm).

4)   The final output series O=(o1, o2, o3......... o2m ) is achieved in the following manner:

o1 = a1 and o2m = bm .In general the formula is as given below: o2i = min(ai+1,bi ) and

o2I+1 = max(ai+1,bi ) for i=1,2,3,4..........m-1.

Now, let us take an example for merging the two sorted series of length 4, i.e., A=(a1, a2, a3, a4) and B=(b1, b2, b3, b4). Assume the numbers of the series are A=(4,6,9,10) and B=(2,7,8,12). The circuit of merging the two given series is illustrated in Figure.

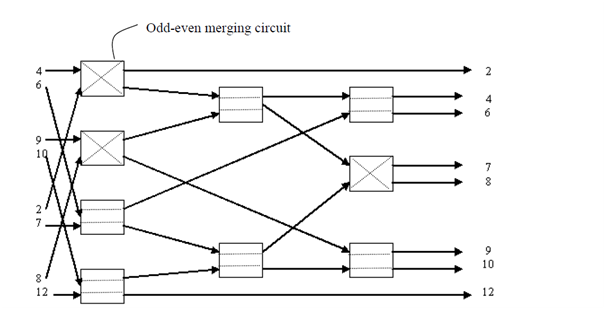
                                                                          Merging Circuit