NPS, NEQ, and DQE of X- Ray Detector
1. An Example of a deterministic blurring. The digital flat panel detectors use discrete pixels to collect scintillation light from the phosphor. Each pixel integrates the light incident to its surface. Suppose the size of the pixel is a. When simplified to 1D case, this stage equivalents to convoluting the input quanta flux q(x) with a rectangular function (1/a) rect (x/a). Find out the MTF of this stage.
2. Phosphor screen of an x-ray imaging detector is exposed to monogenic 50keV x-ray. The absorption efficiency of x-ray photon is 50%. The absorption is assumed only through photoelectric effect and ignores the k-x-ray escape. Thus, each absorbed x-ray will have an average of 100 scintillation light photons coming out of the phosphor. The blurring due to light scatter and spreading can be described by a MTF curve showing in the figure. The scintillation light photons are to be collected by a photo sensor, which have an efficiency of 40%. The average incident flux of 50 keV x-ray quanta is 1000 quanta/mm2 (q0)
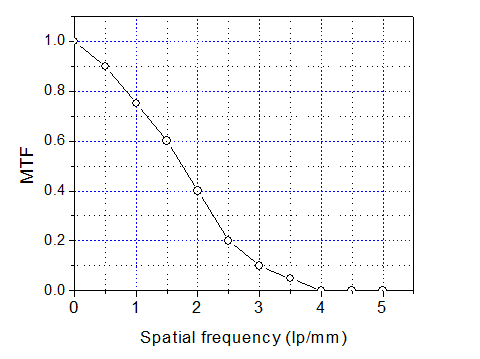
Please calculate the NPS, NEQ, and DQE of this x-ray detector at spatial frequency of 0 and 2.0 line-pair/mm.
(You should use a cascaded system to describe the phosphor. Calculate the NPS and NEQ after each stages, you only need to calculate DQE after last stage)
The tricks to solve this problem are:
1. Break the system down to cascaded stages and identify the type of each stage.
2. Write down the character of each stage: average gain, variance of gain and MTF.
3. Start from the first stage (incident x-ray) and transfer (or prorogate) the quanta (q), NPS, SNR and NEQ through the stages, until you reach the last stage.
4. VERY IMPORTANT! The quanta q, NPS and NEQ output from the previous stage will be the input quanta, NPS, and NEQ of the next stage.
5. Calculate DQE by the ratio of NEQ_out of the last stage to the NEQ_in of the first stage.