Model with Stock Effects
Extraction costs could depend upon the remaining stock in several possible ways. When most of the original stock becomes depleted, total and marginal extraction costs will increase based upon physical difficulties of extracting remaining quantities. Lower stock may also increase costs independent of the extraction rate, as reductions in remaining stock of water in an aquifer or intense mining leads to subsidence of overlying land. In addition, in earlier phases of resource extraction "learning by doing" could decrease costs as experience with a deposit is gained. If that experience comes about through extracting the resource, then costs can be modeled as declining endogenously with reductions in remaining stock. Using discrete time model, the Lagrangian function can be expressed as
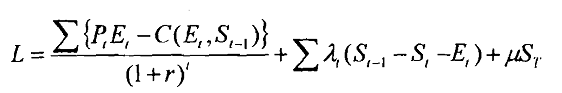
and the first order conditions are
Equation 1
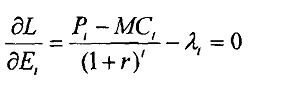
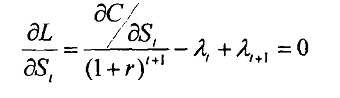
Based on the first order condition above we find that
Equation 2
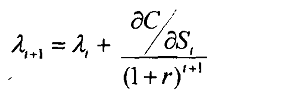
The third first order condition gives us
Equation 3
μST = 0
And implies that λTST = 0
By combining equation 2 and 3 we find that when λt = 0
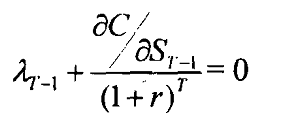
By re-arranging terms in the above, we find that
Equation 4
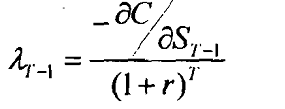
The equation 2 implies that whether the opportunity cost increases or decreases over time depends on the sign of
∂C / ∂St.
There are two possibilities
If ∂C / ∂St < 0 (normal case), then the current value opportunity cost may increase or decrease. However, even if it increases, its growth rate is lower than 'r'.
If ∂C / ∂St > 0 (learning through experience), then the current value opportunity cost growth rate is faster than ‘r’ and the present value increases over time.
The second term on the right hand side of equation 2 is the present value of future cost increase due to one unit additional extraction at time 't'. The essence of this model is, opportunity cost exists even if the resource is ultimately not depleted. This is in sharp contrast to the results of the model without stock effects where positive opportunity cost exists only if the stock is completely depleted within the time horizon.