Linear Approximation Method
This is a rough and ready method of interpolation and is best used when the series moves in predicted intervals. It can be applied to interpolate values in both ascending and descending series. The method can be best described with the help of illustrations.
Example
The sales in units of a consumer durable are ascertained as follows:
|
Year
|
1986
|
1987
|
1988
|
1990
|
|
Sales Units (in '000s)
|
8
|
16
|
24
|
40
|
|
The records of sales for the year 1989 were accidentally lost in a fire. The sales in this year could be interpolated by the following procedure:
-
Use the value of the immediately preceding year as the base value or starting value. We may connote this as base value.
The year immediately preceding 1989, is 1988. Hence 24,000 units sold in 1988 is the base value.
-
Ascertain whether the series is an ascending one or a descending one.
In the illustration, since demand for the units is steadily increasing, we may conclude that it is an ascending series.
-
Find out the difference in values of the variable corresponding to the immediately succeeding and preceding years of the year for which the value is to be interpolated. We may connote this as upper limit minus lower limit.
Value corresponding to the immediately succeeding year (1990) = 40,000 units
Value corresponding to the immediately preceding year (1988) = 24,000 units
Upper limit - Lower limit = 40,000 - 24,000
= 16,000
-
Find out the time interval between the two known values. We may denote this as ts - tp.
In the above illustration, the time interval between 1988 and 1990 is 2 years.
-
Find out the time interval between the immediately preceding year and the year for which the value is to be interpolated. We may denote this as ti - tp.
Time interval between 1988 and 1989 is one year.
-
Interpolate the value as follows:
For the illustration, the sales for the year 1989 will be,
|
24000 +
|
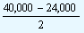 |
x 1 |
= 24,000 + 8,000 = 32,000
If the series is a descending series, the formula will be,
| Base Value - |
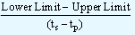 |
x (ti - tp) |