Learning Abilities of Perceptrons - Artificial intelligence

Computational learning theory is the study of what concepts specific learning schemes (representation and method) can and cannot learn. We do not look at this in detail, but a popular example, at first highlighted in a very powerful book by Minsky and Papert involves perceptrons. It has been mathematically verified that the above technique for learning perceptron weights will converge to a ideal classifier for learning tasks where the target concept is linearly separable.

To understand what is and what is not a linearly separable target function, we take simplest functions of all, Boolean functions. These take 2 inputs, which are either -1 or 1 and output either a -1 or a 1. Note down that, in other contexts, the values 1and 0 are used instead of 1 and -1. As an instance function, the AND Boolean function outputs a 1 only if both inputs are 1, whereas the OR function just outputs a 1 if either inputs are 1. Clearly, these relate to the connectives we studied in first order logic. The following 2 perceptrons may represent the AND and OR Boolean functions respectively:

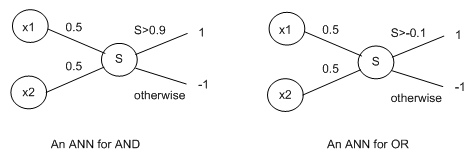
One of the main impacts of Minsky and Papert's book was to highlight the issue that perceptions can't learn a specific boolean function called XOR. This function output 1 if the 2 inputs are not the similar. To see why XOR can't be learned, try and write down a perception to do the task. The following diagram highlights the notion of linear reparability in Boolean functions, which describe why they cannot be learned by perceptions:

In every case, we have plotted the values taken by the Boolean function when the inputs are specific values: (-1,-1) ;(1,-1);(-1,1) and (1,1). For the AND function, there is just one place where a 1 is plotted, namely when both inputs are 1. It meant that we could draw the dotted line to separate the output -1s from the 1s. We were able to draw a same line in the OR case. Because we may draw these lines, we say that these functions are linearly separable. Notice that it is impossible to draw such as line for the XOR plot: wherever you try, you never get a clear split into 1s and -1s.

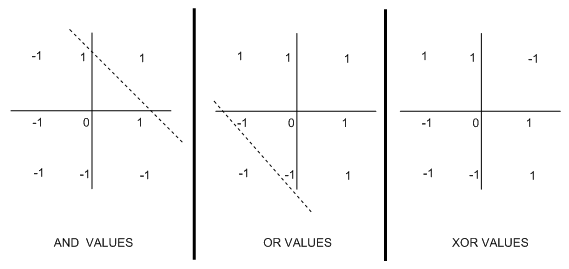
The dotted lines may be seen as the threshold in perceptrons: if the weighted sum S falls below it, then the perceptron outputs 1 value, and if S falls above it, the other output is produced. It is not issue how the weights are organized; the threshold will yet be a line on the graph.  Therefore, functions which are not linearly separable can't be represented by perceptrons.

Notice that this result extends to functions over any number of variables, which may take  in  any  input,  but  which  produce  a  Boolean  output  (and  so could,  in principle be learned by a perceptron). In the following two graphs, For example, the function takes in 2 inputs (like Boolean functions), but the input may be over a range of values. The concept on the left may be learned by a perceptron, whereas the concept on the correct cannot:

As an exercise, draw in the separating (threshold) line in the left hand plot.

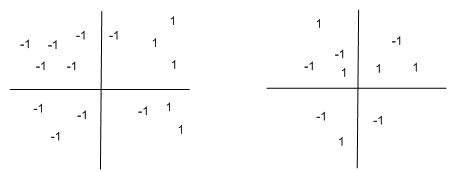
Unluckily, the disclosure in Minsky and Papert's book that perceptrons can't learn even sach type of simple function was taken the incorrect way: people believed it represented a basic flaw in the use of ANNs to perform learning job. This lead to a winter of ANN research within Artificial Intelligence, which lasted over a decade. In realism, perceptrons were being studied in order to achived insights into more complexed architectures with hidden layers, which don't have the restriction that perceptrons have. No one ever advised that perceptrons would be eventually used to solve real world learning problems. luckily, people studying ANNs within other sciences (notably neuro-science) revived interest in the study of ANNs. For more facts of computational learning theory, see chapter 7 of Tom Mitchell's machine learning book.