Laspeyres index

The Laspeyres index tells us that:

- The amount of money at present year prices which an individual requires to purchase bundle of goods and services which was selected in base year divided by cost of purchasing same bundle at the base year prices.

* Computing Raheela's Laspeyres cost of living index 

- Setting quantities of goods in the year 1997 equal to what were bought by her sister, but setting the prices at their 1997 levels result in expenditure of 

$1,720 (100 x 2.20 + 15 x $100)

*  The cost of living of her adjustment would be $1,220.

* The Laspeyres index is:  $1,720/$500 = 344.

*  This overstates true cost of living increase.



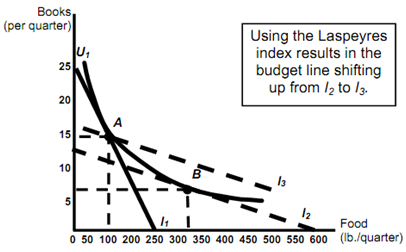
What Do You Think?

- Does the Laspeyres index overstate the true cost of living index always? ? Yes!

- The Laspeyres index supposes that consumers do not alter their consumption patterns as the prices change.

- By increasing purchases of those items which have become comparatively cheaper, and decreasing purchases of relatively more expensive items consumers can achieve same level of utility without having to consume the same amount of goods.

*  The Paasche Index

- Computes the amount of money at current year prices which an individual requires to purchase a current amount of goods and services divided by cost of purchasing same bundle in base year.

*  Comparing Two Indexes

- Assume:

- Two goods: Food (F) and Clothing (C)

*  Comparing the Two Indexes 

- Suppose:

• P_Ft & P_Ct be current year prices

• P_Fb & P_Cb be base year prices
• F_t & C_t be current year quantities
• F_b & C_b be base year quantities

- Both the indexes involve ratios which involve today's present year prices, P_Ft and P_Ct.

- Although, the Laspeyres index depends on the consumption of base year, F_b and C_b.

- While, Paasche index relies on today's present consumption, F_t and C_t .

* Then the comparison of Laspeyres and Paasche indexes gives following equations:

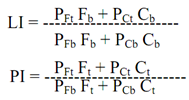
- Sarah (1990)

• Cost of base year bundle at the current prices equals

             $1,720 (100 lbs x $2.20/lb + 15 books x $100/book)

• Cost of same bundle at the base year prices is

             $500 (100 lbs x $2.00/lb + 15 books x $20/book)

- Sarah (1990)



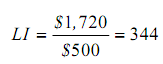
• Cost of buying current year bundle at the present year prices is

             $1,260 (300 lbs x $2.20/lb + 6 books x $100/book)

• Cost of same bundle at the base year prices is 

             $720 (300 lbs x $2/lb + 6 books x $20/book)


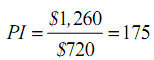
The Paasche index will understate cost of living as it assumes that individual will buy the present year amount in the base year.