The Null Hypothesis - H0:  There is autocorrelation

The Alternative Hypothesis - H1: There is no autocorrelation

Rejection Criteria: Reject H0 (n-s)R² >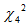 = (1515 - 4) x (0.01) = 15.11 > 9.49 ()

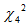1515 cases used, 4 cases contain missing values

Since 15.11 > 9.49 the chi-squared value with 4 lags (ET-1, ET-2, ET-3, and ET-4) there is evidence to suggest that we reject H0 meaning that there is no autocorrelation.    

The regression equation is

RESI1 = - 0.0011 + 0.000005 totexp - 0.000001 income + 0.000017 age + 0.00007 nk

        + 0.0085 ET-1 + 0.0070 ET-2 - 0.0284 ET-3 - 0.0074 ET-4

Predictor         Coef     SE Coef                 T      P

Constant       -0.00105     0.01375        -0.08  0.939

totexp          0.00000471  0.00006080   0.08  0.938

income        -0.00000082  0.00004314  -0.02  0.985

age              0.0000167   0.0003090     0.05  0.957

nk                0.000071     0.004785       0.01  0.988

ET-1             0.00847       0.02580         0.33  0.743

ET-2             0.00700       0.02584         0.27  0.786

ET-3           -0.02842       0.02587        -1.10  0.272

ET-4          -0.00743       0.02592         -0.29  0.774

As the T value decreases, the P value increases which is noticeable above due to the inclusions of lags. Most of the T values are now closer to 0 which shows that there is less reliability of the coefficient.  ET-3 will be included in a further regression analysis as it is significant with a value of -1.10, conversely ET-1, ET-2, ET-4 will be removed as they are insignificant with low T values.     

S = 0.0905514   R-Sq = 0.1%   R-Sq(adj) = 0.0%

The inclusion of lags has caused the r-squared to be really low at 0.1% which certainly suggests that the model is inadequate for explaining the Y variable. It also indicates that data points are distributed away from the line of best fit and that the independent variables are poor predictors for the dependent variable. The remaining percentage (99.9%) is the variation which is unknown.

Analysis of Variance

Source               DF         SS        MS     F      P

Regression        8    0.012127  0.001516  0.18  0.993

Residual Error  1506  12.348529  0.008200

Total                1514  12.360656

Source  DF    Seq SS

totexp   1  0.000029

income  1  0.000005

age       1  0.000011

nk         1  0.000000

ET-1      1  0.000903

ET-2      1  0.000544

ET-3      1  0.009961

ET-4      1  0.000673

Since the F value is small at 0.18 and the P value is high 0.993 it reveals that there is no relationship between the Y dependent variable and X independent variables. This indicates that as it is 0.18 it does not support the model and therefore the slopes are equal to 0.