Interest Rate Calculations
In considering the time value of money, it is convenient to represent mathematically the relationship between the current or present value of a single sum, which we will represent as P, and its future value (F) in n years.
F = P + In
where In is the increase in the value of P over n years, which is a function of an annual interest rate (i).
The are two approaches for computing In. The first approach known as simple interest rate considers In to be a linear function of time, which is given by,
In = Pin
and
Fn = P(1 + in)
The second approach known as compound interest rate, considers that at the end of each interest period the accumulated amount of money is now the amount of principal at the end previous period plus the interest accumulated over that period P(l + i); therefore, for the subsequent period the accumulated amount of money will be P(P + i)i. Now, using the same procedure we can fill Table 2.1 for the subsequent periods.
Table Derivation of equation 1
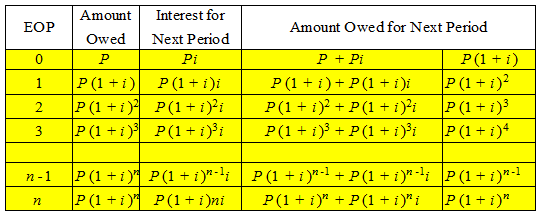
Thus, we can derive the formula for the future amount F, in terms of P, i, and n given by,
F =P(l+i)n