Integral Test- Harmonic Series

In harmonic series discussion we said that the harmonic series was a divergent series.  It is now time to demonstrate that statement.  This proof will as well get us started on the way to our next test for convergence that we will be looking at.

 Thus, we will be trying to verify that the harmonic series,

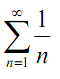
We'll initiate this off by looking at an apparently not related problem.  Let us start off by asking what the area under f (x) =1/x on the interval [1, ∞).  From the segment on Improper Integrals we come to know that this is,

∫^∞₁ 1/x (dx) = ∞

and thus we called this integral divergent.

Thus, just how does that help us to demonstrate that the harmonic series diverges? Well, remind that we can all time estimate the area by breaking up the interval into segments and then drawing in rectangles and using the sum of the area all of the rectangles as an approximation of the actual area. Let us do that for this problem also and see what we acquire.

We will divide the interval into subintervals of width 1 and we will take the function value at the left endpoint as the height of the rectangle. The diagram below illustrates the first few rectangles for this area.

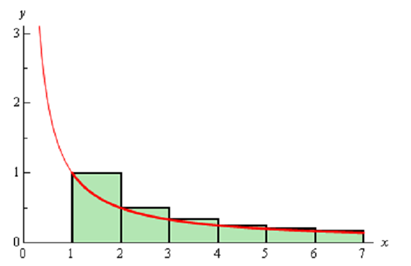
Thus, the area under the curve is approximately,

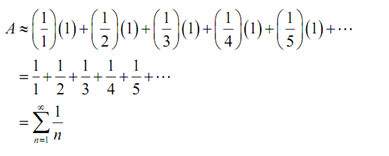
Now note some things about this approximation.  1^st, each of the rectangles overestimates the actual area and 2^nd the formula for the area is precisely the harmonic series!