In 1952, to provide equilibrium between assets and liabilities of insurance companies, Frank Redington, an English actuary, proposed interest rate immunization technique. Later in 1971, the same concept was extended to bond portfolios by Fisher and Weil.

A variation in interest rate will result in two opposite effects. An increase in the interest rates will decrease the value of bond portfolio, but leads to higher return on the coupons reinvestment. The basic mechanism underlying the concept of portfolio immunization is 'portfolio structure'. A portfolio structure balances the change in the value of the portfolio at the end of the investment horizon with the returns from the reinvestment of portfolio coupons payments. Thus, immunization can be defined as a process of offsetting price risk and reinvestment risk.

For example, let us assume that an investor is holding a bond with 5 years maturity and 8 percent coupon rate at a price (quoted) of Rs.108.42. The yield of bond is 6 percent. The investor wants to know the final wealth for different time horizons in case some unexpected variation occurs in the market yield today (the market yield would remain stable after this).

The results for 1 to 5 years time-horizons, and 4% to 8% final market yield (i.e., a variation of ±2%) can be seen in the following table:

Table 1: The Effect of a Yield Variation on Terminal Wealth

The above results are shown in the form of graph in the following figure:

Figure 2: The Effect of a Yield Variation on Terminal Wealth

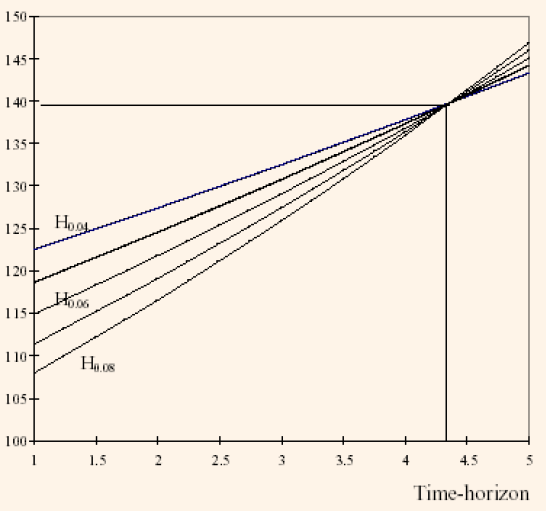
The final wealth differs slightly from the status quo assumption (in the absence of variation we would be on the curve H_0.06). On short time-horizon, the effect on the bond price is higher when compared to the effect on the reinvestment of the coupons and the investor wishes to avoid an increase in interest rate. In the case of longer time-horizons, the reinvestment of coupons grabs a higher part of the final wealth and the investor tries to avoid decrease in interest rate.

An interesting point to be noted here is, there appears to be a time horizon
(4.34 years) for which the final wealth will be the same, whatever the initial interest rate variation may be. If such a time-horizon is selected, it will result in 6% yield and a final wealth of:

W=108.42(1.06)⁴³⁴=139.64

Now, the portfolio is said to be immunized against interest rate variations. It can be shown theoretically that time-horizon is the duration of the bond that is considered. Thus, an investor can avoid interest rates variations if he selects a portfolio with duration equal to its time horizon.

The major problem here is, time-horizon is not a variable, but it is a given value. That means, the investor will not modify the time-horizon to immunize the portfolio, but he will be given a time-horizon for which he has to immunize the portfolio. Now, let us see how to select a set of securities whose stream of cash flows has duration equal to the time horizon of the investor.

It might sound simple to do so, by just creating a portfolio with duration equal to the time horizon of the investor (because portfolio duration is the weighted average of the durations of the individual issues):

         Duration = Time Horizon (= TH)

However, the above condition alone is not sufficient for our purpose:

• As discussed earlier, duration does not change continuously with the lapse of time, but the investor's time horizon declines continuously with the lapse of time. So, in order to ensure that duration and time-horizon remain equal, a portfolio has to be balanced whenever there is a liability payment due.

• Whenever there is an interest rate modification, an immunized portfolio is not immunized further, as its duration gets modified. For this reason, every portfolio should be theoretically rebalanced after each change in interest rates.

• Lastly, the coupon payment modifies the portfolio duration in a non-linear form. Further, their reinvestment may also affect the immunization equilibrium.

Because of all the above reasons, immunization has to be a dynamic process. To serve this purpose, the portfolio to be immunized should be written as:

Duration_t=Time horizon_t (for all t)

The portfolio must be frequently rebalanced to satisfy this condition.