Illustration of Marginal profit

To illustrate the computations, suppose that the marginal profit or XE in our model is changed from 3 to 3 + δ1, where δ represents either positive or negative change. This means that the objective function reads as: Z = (3 + δ1) X_E + 2X_I.

If we use this information in the starting tableau and carry out the same arithmetic operations used to produce the optimum tableau, the optimum Z equation will appear as:

This equation is the same as the optimum Z equation before the change δ₁ is effected, modified by terms of δ₁. The coefficients of δ₁ are essentially those in the X_E equation of the optimum tableau, which are

Pivot Element

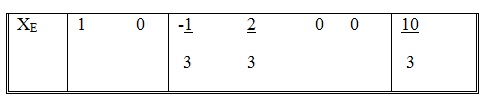
We choose the X_E equation because XE is the variable whose objective coefficient is being changed by δ₁.

The change δ₁ will not affect the optimality of the problem as long as all the Z equation coefficients of the non-basic variables remain non-negative (maximization) that is:

1/3 - δ₁/3 ≥0

4/3 + 2δ₁/3 ≥ 0  

First Relationship  shows that δ₁ ≥ 1 and the relation second yields δ₁ ≥ -2.  Both relations limit δ₁ by -2 ≤ δ₁ ≤ 1. This means that the coefficient of XE can be as small as 3 + (-2) = 1 or as large as 3 + 1 = 4 without causing any change in the optimal values of the variables. The optimal value of Z, however, will change according to the expression 12 2/3 + 10/3 δ₁ where -2 ≤ δ ≤ 1.

The foregoing discussion assumed that the variable whose coefficient is being changed has an equation in the constraints. This is true only if the variable is basic (such as X_E and X_I above). If it is non-basic, it will not appear in the basic column.

The treatment of non-basic variable is straight forward. Any change in the objective coefficient of a non-basic variable will affect only that coefficient in the optimal tableau. To illustrate this point, consider changing the coefficient of SI (the first slack variable) from 0 to 0 + δ₃. If you carry out the arithmetic operations leading to the optimum tableau, the resulting Z equation becomes:

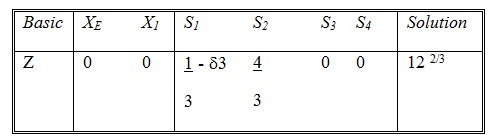
It shows that the only change occurs in the coefficient of SI, where it is decreased by δ3. As a general rule, then, all we have to do in the case of a non-basic variable is to decrease the Z coefficient of the non-basic variable by the amount by which the original coefficient of the variable is increased.