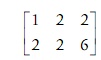Illustration of Gauss elimination:

For illustration, for a 2 × 2 system, an augmented matrix be:

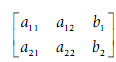
Then, the EROs is applied to obtain the augmented matrix into an upper triangular form:

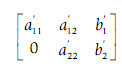
Therefore, the goal is simply to substitute a₂₁ with 0. Here, the primes points that the values (might) have been changed.

Putting this back into the equation form results,

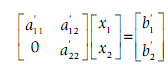
Executing this matrix multiplication for each row outcomes in:

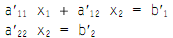
Therefore, the solution is as shown below:

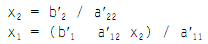
Likewise, for a 3 × 3 system, the augmented matrix is decreased to upper triangular form:

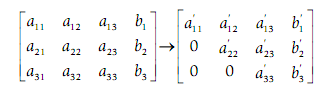
(This will be completed systematically by first obtaining a 0 in the a₂₁ position, then a₃₁, and lastly a₃₂.)

Then, the answer will be:

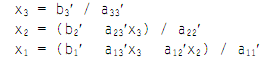
As an illustration, consider the 2 × 2 system of equations as shown below:

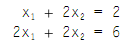
As a matrix equation Ax = b, this is:

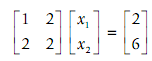
The initial step is to augment the coefficient matrix A with the b to obtain an augmented matrix [A| b]: