The ID3 algorithm

The calculation for information gain is the very difficult phase of this algorithm. ID3 performs a search whereby the search states are decision trees and the operator includes adding a node to an appearing tree. It uses information gain to measure the feature to put in each node, and performs a greedy search using this measure of worth. The algorithm goes as follows:

Given a group of examples, S, categorized in categories ci, then:

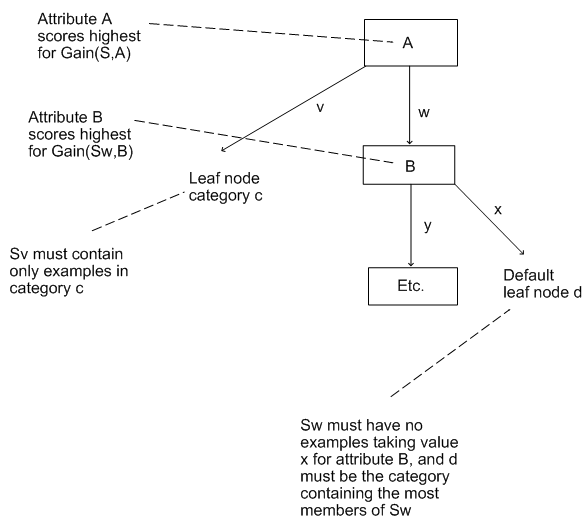
1.  Select  the  root  node  to  be  the  feature,  A,  which  scores  the  highest  for information gain relates to S.

2. For every value v that A may probably take, draw a branch from the node.

3. For every branch from A consequent to value v, calculate Sv. Then:

    If Sv is empty, select the category cdefault which includes the maximum examples from S, and keep it as the leaf node category which terminates that branch.

• If Sv includes only examples from a category c, then keep c as the leaf node category which terminates that branch.
• Otherwise, avoide A from the set of features which may be keep into nodes. Then put a new node in the decision tree, where the new feature being checked in the node is the one which scores maximum for information gain relates to Sv (note: not relative to S). This new node arise the cycle again (from 2), with S changed by Sv in the calculations and the tree built iteratively like this.

The algorithm ends her when all the features have been bushed, or the decision tree absolutely classifies the examples.

The following diagram must describe the ID3 algorithm further: