Graphical Solution Procedure sample assignment and solved questions, free examples and solved homework samples for Graphical Solution Procedure in operation research.

Question: Max Z = 80x₁ + 55x₂

Subject to

4x₁+ 2x₂ ≤ 40

            2x₁ + 4x₂ ≤ 32

 x₁ ≥ 0 , x₂ ≥ 0

Answer

The first constraint 4x₁+ 2 x₂ ≤ 40, can be written in a form of equation

4x₁+ 2 x₂ = 40

Place x₁ =0, then x₂ = 20

Place x₂ =0, then x₁ = 10

Therefore, the coordinates are (0, 20) and (10, 0)

The second constraint 2x₁ + 4x₂ ≤ 32, can be written in a form of equation

2x₁ + 4x₂ =32

Place x₁ =0, then x₂ = 8

Place x₂ =0, then x₁ = 16

Therefore, the coordinates are (0, 8) and (16, 0)

The graphical presentation is

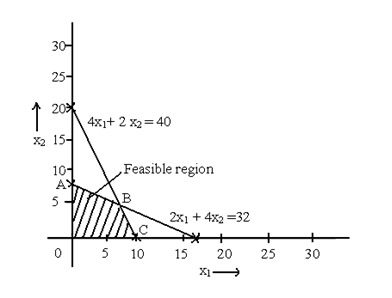
The corner positions of feasible region are A, B and C. Thus the coordinates for the corner points are

A (0, 8)

B (8, 4) (Crack the two equations 4x₁+ 2 x₂ = 40 and 2x₁ + 4x₂ =32 to obtain the coordinates)

C (10, 0)

We are given that Max Z = 80x₁ + 55x₂

At A (0, 8)

Z = 80(0) + 55(8) = 440

At B (8, 4)

Z = 80(8) + 55(4) = 860

At C (10, 0)

Z = 80(10) + 55(0) = 800

The maximum value is achieved at the point B. Thus Max Z = 860 and x₁ = 8, x₂ = 4