We should graph a couple of these to make sure that we can graph them as well.
Example: Sketch the graph of the following piecewise function.
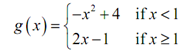
Solution
Now while we are graphing piecewise functions we are in fact graphing various functions at once, except we are just going to graph them on very particular intervals. In this case we will be graphing the given two functions,
- x2 + 4 on x < 1
2 x -1 on x ≥ 1
We'll have to be a little careful with what is going on right at x =1 as technically that will only be valid for the bottom function. But, we'll deal along with that at the very end while we actually do the graph. For now, we will employ x = 1 in both functions.
Here the first thing to do is to get a table of values for each function on the particular range and again we will employ function. x = 1 in both even though technically it only have to be used with the bottom
|
x
|
- x2 + 4
|
( x, y )
|
|
-2
|
0
|
(-2, 0)
|
|
-1
|
3
|
( -1, 3)
|
|
0
|
4
|
(0, 4)
|
|
1
|
3
|
(1, 3)
|
|
x
|
2 x -1
|
( x, y )
|
|
1
|
1
|
(1,1)
|
|
2
|
3
|
( 2, 3)
|
|
3
|
5
|
(3, 5)
|
Following is a sketch of the graph and notice how we indicated the points at x = 1 . For the top function we utilized an open dot for the point at x = 1 and for the bottom function we utilized a closed dot at x = 1 . In this way we make it apparent on the graph that only the bottom function actually has a point at x = 1 .
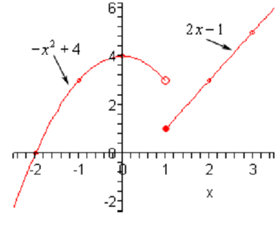
Notice that as the two graphs didn't meet at x = 1 we left a blank space in the graph. Do not connect these two points along a line. There actually does have to be a break there to indicate that the two portions do not meet at x = 1 .
Sometimes the two portions will meet at these points & at other times they won't. We have not ever expected them to meet or not to meet till we've in fact sketched the graph.