Forces in the members of the truss:

Find out the forces in the members AB, BC, AC of the truss shown in the figure drawn adjacent.

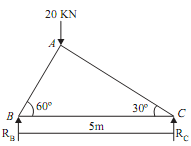
Sol.: First determine the reaction R_B  and R_C. The line of action of load is 20KN which is acting at A is vertical. This load is at a distance of AB cos 60º, from point B. Now let us find out distance AB, The ?ABC is a right angle triangle having angle BAC = 90º. Thus AB will be equal to CB cos60º. AB = 5 X cos 60º = 2.5m Now distance of line of action of 20KN from B is = AB cos 60º = 1.25m

Now, taking moment about B, we get

R_C X 5 - 20 X 1.25 = 0

R_C = 5KN                                     ...(i)

R_B = 15KN                                  ...(ii)

Let the forces in member AC, AB and BC is in tension.

Now consider the equilibrium of the various joints.

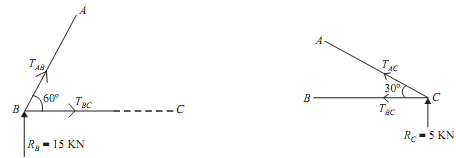
Joint B:

Consider free body diagram of joint B as shown in figure(a) Assume,

T_AB  = Force in member AB

T_BC  = Force in member BC

Direction of both the forces is taken away from B. As the three forces are acting at joint B. So

apply lami's theorem at point B.

T_AB/sin270º = T_BC/sin30º = RB/sin60º

T_AB/sin270º = T_BC/sin30º = 15/sin60º

By solving

Joint C Figure(b)

Consider free body diagram of joint C as shown in figure (b) Let,

T_BC  = Force in member BC
 T_AC  = Force in member AC

The direction of both the forces is taken away from the joint C. As the three forces are acting at joint C. Thus apply lami's theorem at point C.

T_BC/sin60º = T_AC/sin270º = R_C/sin30º

T_BC/sin60º = T_AC/sin270º = 5/sin30º

By solving

T_AC  = -10KN                                                                                                                      ...(v)

T_AC  = 10KN (Compressive)                                    .......ANS