Find the normal stress:

Figure 1 shows the projection of a rectangular prism ABCD, formed by adhesive bonding of two triangular prisms ABC and ACD. The state of stress in the prism is given by the components σ_x = 40 N/mm², σ_y = 0 and τ = 0.

If the shear and tensile strengths of the adhesive are 10 N/mm² and 12 N/mm², verify the safety of the joints and find out the value of σx at which the joint will fail.

Solution

The aspect angle θ of the bonding plane AC

= 90^o  + tan^-1 (50/75) = 90^o = 33.69^o = 123.69^o

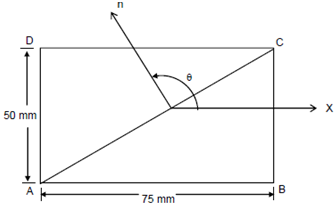
Figure

Known stress components are as follows:

σ_x = 40 N/mm², σ_y = 0 and τ_xy = 0

Stress components on plane AC,

Normal stress, σ_n  = σ_x  cos2  θ

= 40 cos² 123.69^o

= 12.3076 N/mm² > 10 N/mm²

Shear stress τ_nt  +-σx/2 sin 2θ

= - 40/2 sin (2 × 123.69^o)

= 18.4615 N/mm² > 12 N/mm²

The tensile stress on plane AC is not inside the tensile strength of the bond. Also, the shear stress on the plane exceeds the shear strength of the bond and hence, the bond will fail both in tensile and shear.

Let us find the normal stress σx that might be safely applied. Shear strength of the bond = 12 N/mm²

Shear stress on bonding plane -σx/2 sin 2θ

∴          12 = - σx/2 sin 247.38^o

σx = 12 ×2 /sin 247.38^o = 26 N/mm²

So the maximum stress we may apply on the plane CB is 26 N/mm². Here, you may note that in strength analysis the sign of the shear stress has no significance, while the sign of the normal stress is important, since the tensile and compressive strengths may differ considerably.