Find the maximum shear stress - stepped circular bar:

A stepped circular bar ABC 4 m long fixed at one of the end 'A' is subjected to a torque of 10 kN-m. If the portion AB is solid shaft of 100 mm diameter & the portion BC is a hollow with an external diameter 100 mm and internal diameter 80 mm. discover the maximum shear stress & maximum angle of twist.

AB = 2 m; BC = 2 m; G = 80 kN/mm².

Solution

G = 80 kN/mm²  = 0.8 × 10¹¹ N/mm²

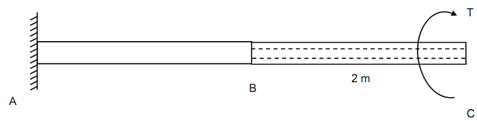
Figure

 Portion BC

l = 2 m, d₁ = 100 mm, d₂ = 80 mm, T = 180 kN-m = 10 × 10³ N-m

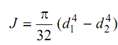
=  π (0.1⁴  - 0.08⁴ ) = 5.8 × 10^{- 6} m⁴

R = 100 = 50 mm = 0.05 m

T / J = τ_max/ R = G θ/ l

τ_max = (T/J) × R =  (10× 10³ )(5.8 × 10^{- 6} ) × (0.05)

= 86.2 × 10⁶ N/mm²  = 86.2 N/mm²

Portion AB

Solid T = 10 kN-m

d = 100 mm

J = ( π / 32 )(0.1)⁴  = 9.8 × 10^{- 6} m4

R = d /2 = 50 mm = 0.05 m

τ _max     = T R / d J = ((10 × 10 ³) (2) / (9.8 × 10^{- 6} ) )(0.05) = 51 × 10⁶ N/m²  = 51 N/mm²

θ= Tl / GJ   = (10 × 10³) (2) / ((0.8 × 10¹¹) (9.8 × 10^{- 6}))

= 2.55 × 10^{- 2} radians

 ∴         Maximum shear stress = 86.2 N/mm²

θ_A = 0

θ_B  = 4.3 × 10^{- 2} radians

θ_C  = 4.3 × 10^{- 2}  + 2.55 × 10^{- 6}  = 6.85 × 10 ⁶ radians