Find out the velocity of the chain:

Figure shows a metal chain ABC where portion BC is of length 0.4 metres and is hanging vertically, & portion AB of length 0.8 metres rests on the rough surface of the horizontal table. The coefficient of friction among chain and table is 0.1. The chain has uniform weight of 20 N/metre of its length. Find out the velocity of the chain when end A just leaves the edge of the table.

Solution

Initial position of chain AB weighs = 0.8 × 20 =16 N

F₀ = Initial frictional force of table = 16 × 0.1 =1.6 N

P₀ = Dragging force due to weight of portion BC = 0.4 × 20 = 8 N

As P₀ > F₀, the chain starts moving outward.

Let A′B′C′ as any intermediate position of the chain throughout its motion as illustrated in Figure (b). Let A′B′ = x, B′C ′ = (1.2 - x) metres.

Frictional Force, F_x = 20 x × μ

WD during small displacement dx = 0.1 × 20 x (dx)

 WD during moving from position A to B′ =

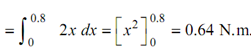
By using the principle of conservation of energy, by adopting datum level as at point C″ at 1.2 m below the table surface.

where, A″ coincides with B.

Supposing velocity of chain as (V) at position (A′ C ′) ;

 (20 × 0.8) × 1.2 + (20 × 0.4) × 1 = 20 × 1.2 × 0.6 + 24 V ² / 2 g + 0.64

i.e.       (PE of AB + PE of BC = PE of ABC while fully hanging + loss)

19.2 + 8 = 14.4 + 0.64 + (12V² /g) + 0.64

∴ V = VA′′ C′′ = 3.15 m/sec.