Find out the reactions at hinge:

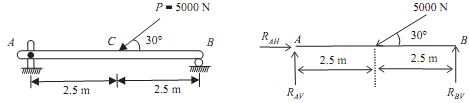
A board ABCD is held in position as shown in Figure by a cable BE and a hinge at A. If the weight of the board is 5 kN, find out the reactions at hinge A and the tension T in the cable.

Solution

Assume the components of the reaction at A be H_A and V_A as illustrated in Figure. The board is at rest under the action of four forces H_A, V_A, T and W.

Taking moments of all of forces about A, we obtain

∑ M _A = 0

                               ∴ - (T sin 30^o) × 1.6 + W × 0.8 = 0

                                 ∴ - 0.8T + 5 × 0.8 = 0

                                  ∴ T = 4 /0.8 = 5 kN

And, ∑ F_x = 0

∴ H _A  - T cos 30^o  = 0

∴ H _A  = T cos 30^o

 (On putting T = 5 kN) ∴ H _A  = 5 × 0.866 = 4.33 kN

Also, ∑ F_y  = 0

                     ∴ V_A  + T sin 30^o  - W = 0

                      ∴ V _A  = W - T sin 30^o

                                  = 5 - 5 × 0.5

                                  = 2.5 kN

Now

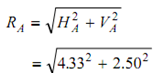
                               = 5 kN

θ = tan ^-1  ( V_A / H _A)

= tan ^-1  (2.50 /4.33)

= 30^o

Reaction R_A has a magnitude of 5 kN and is inclined at 30^o to the horizontal.

[Note : You can attempt the same problem considering the board to be subjected to 3 forces only viz., R_A, T and W. As three of the forces keep the body at rest, these should be concurrent. Find the point of concurrence and get the values of unknowns RA and T, using

                  ∑ F_x  = 0   and             ∑ F_y  = 0

knowing the direction of R_A, you might also use Lami's theorem either.]