Find out the impact-force:

A mass of 3 kg ball freely falls from a height of 2 metres on an anvil, & rise 0.5 metre after the blow. If the duration of impact is (1/50)^th  of a second, find out the impact-force (i.e. Force because of  impact) on the mass. State the total reaction offered by the anvil on the mass.

Solution

H₁ = Fall of the ball = 2 m

Suppose vertically upward direction as the direction for all the vectors such as momentum forces etc.

V1  = Initial velocity of ball just before impact on the anvil. (Downward direction implies - ve)

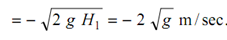
H ₂  = Rising of the ball after impact = 0.5 m

V₂  = Upward velocity (i.e. + ve) after impact

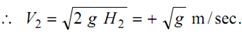
Mass of the ball (m) = 3 kg.

F × dt = Change in momentum  = m (V₂  - V₁ )

Impact force on the mass = m (V₂  - V₁ ) /(dt )

= 3 (3 √g ) × 50

= 450   √g  N.

Impact force on the anvil is downward

= - 450 √g Newtons;

where g = 9.8 m / sec² .

Considering weight of mass W = 3 × 9.8 ≈ (30) N or  (3 g ) N the total upward reaction at Anvil = (450 √g + 30) N.