Find out the forces in the members of the tower:

Find out the forces in the members of the tower.

Solution

By symmetry, ∠ AFG = ∠ AGF = θ and HG = 7.5 m; while AH = 3 × 5 = 15 m.

∴  

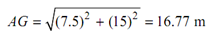
cos θ= 7.5 /AG =  7.5 /16.77 = 0.4472

 (∴ θ = 63.434 degrees)

 and,  sin θ=   15/16.77  = 0.8944

Letting the equilibrium of joint A (and, supposing f_AB and f_AC both to be tensile), and resolving forces horizontally and vertically, we obtain:

10 + f _AC cos θ - f _{AB cos} θ = 0        --------- (i)

And    f _AB sin θ+ f _AC sin θ= 0            -------- (ii)

From (ii), f _AB = - f _AC

and, thus, from (i)

10 + 2 f _AC cos θ = 0

∴          f _AC  =-  5 /0.4472

                     = - 11.1806 t

 (- ve sign indicating f_AC is under compression and f_AB = + 11.1806 t (that means tension).

Joint B

Suppose both f_BC and f_CD to be both tensile; and resolving forces at right-angles to AD:

                 F_BC sin θ= 0 ⇒ ∴ f _BC = 0

Hence, f _AB = f _BD = 11.1806 t(i.e. tensile).

Joint C

Suppose forces f_CD and f_CE to be both tensile, and resolving all the forces at right angles to AE (taking ∠ DCE = α).

 f_CD sin α= 0 ⇒  ∴ f_CD  = 0

 Since both f_BC and f_CD are equal to zero:

f_CE = f _AC  = 11.1806 t(comp.)

Joint D

Suppose f_DE and f_DF both to be tensile and resolving out forces at right-angles to BF:

f _DE  sin θ= 0 ⇒  ∴ f _DE  = 0

As f_CD  = f _DE  = 0 ⇒  ∴ f _DF   = f _BD  = 11.1806 t

Joint E

Assume f_EF and f_EG to be both tensile, and resolving forces at right-angles to CG :

f _EF  sin α= 0   ⇒ f _EF   = 0

∴ f _EG  = f_CE  = 11.1806 t (comp.)

 (a)       A frame illustrated in Figure is supported by a hinge at A and a roller at E. Compute the horizontal & vertical components of hinge forces at B and C as they act upon member AC.