Find out the centroid of the shaded :

Find out the centroid of the shaded area shown in Figure

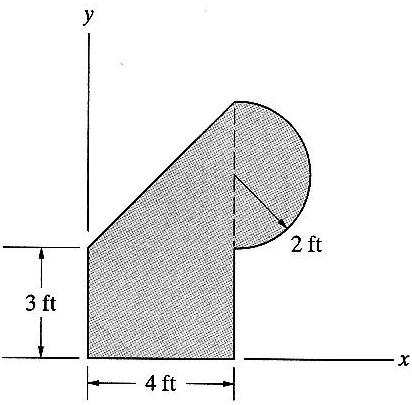
Solution

Net area of shaded portion of Figure

= The area of full circle of radius r (A₁) -   the area of cut out circle of radius r/2 ( A )

= π r ² - π r ² / 4 = 3 π r ² / 4

 Area A₂ is to be considers as negative area.

Let moment of areas around G (the needed C. G.); ∑ A_i x_i = 0 since the lever-arm of the Resultant area A regarding G is zero,

A₁  x₁ + (- A ₂ ) x₂  =  A × (0) = 0

∴ π r ²  (- x) + ( - π r ² /4)    × (- (r/2)+  x¯ )} = 0

 (an anticlockwise moment)   (an anticlockwise moment)

∴ -  (3 π r /4 ) x¯ +   π r³/(4 × 2) = 0

∴ x¯ = +  r/6

Positive sign of x show that with respect to the origin O of reference axes x and y, x¯ = OG is along with positive direction of x axis. As the centres O and A of the two area (A₁) and (- A₂) are taken along x axis; G lies on AO.