Find maximum torque which can be transmitted by belt drive:

A belt is stretched over the two identical pulleys having diameter D meter. The initial tension in belt throughout is 2.4KN when pulleys are at rest. In using these pulleys and belt to transmit torque, it is seen that the increase in tension on one side is equal to decrease on the other side. Find maximum torque which can be transmitted by belt drive, given that the coefficient of friction between the belt and the pulley is 0.30.                                                      

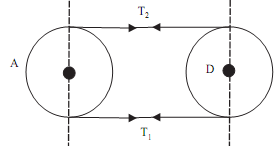
Sol: Given:

Diameter of both the pulley = D

Initial tension in belt (T_O) =2.4KN Torque = ?

Coefficient of the friction (µ) = 0.3

Since diameter of both pulley are same, that is, Angle of contact = Π

T_O  = (T₁  + T₂)/2

T₁  + T₂  = 4.8KN                                                                                                                             ...(i)

Now, Ratio of belt tension = T₁/T₂  = e^µθ

T₁/T₂  = e^(0.3)Π

T₁=2.566T2                                                                                                                                 ...(ii)

Putting value of (ii) in equation (i), We get

T₁  = 3.46KN                                                                                  .......ANS

T₂  = 1.35KN     .......ANS

Now, The maximum torque transmitted by pulley = (T₁  - T₂)D/2 (As radius of both pulley are same)

Torque = (3.46 - 1.35)D/2 = 1.055D KN-m

Torque =   1.055D KN-m                                                                    .......ANS