Find Dispersion Relation for Free Electron

Question: Find the dispersion relation for a free electron, and, thus, observe the relation between its rest mass and effective mass.

Solution: For a free electron, the electron momentum is  p =m₀v = hk. Thus, E=m₀V²/2=p²/ (2m₀) = h²k²/(2m₀). Therefore, the dispersion relation, i.e., E-k relation is parabolic. Hence, m^x = h²/∂²Ε/∂K²=m₀. This is a very interesting relation that says states that for a free electron, the rest mass and effective mass are one and similar, which is because of the parabolic band structure. Several materials have non-parabolic E-k relation, and, so they have quite different rest mass and effective mass for electrons.

Note: the effective mass may become a function of energy, for severely non-parabolic band structures, however, near the minima of the conduction band and towards the maxima of the valence band, the band structure can be taken to be parabolic, and, thus, an effective mass, which is independent of energy, may be obtained.

• Thus, the effective mass is an inverse function of the curvature of the E-k diagram: weak curvature gives large mass, and strong curvature gives small mass.
• Note that in general, the effective mass is a tensor quantity, however, for parabolic bands, it is a constant.
• Another interesting feature is that the curvature d²E/dk² is positive at the conduction band minima, however, it is negative at the valence band maxima.
• Thus, the electrons near the top of the valence band have negative effective mass.
• Valence band electrons with negative charge and negative mass move in an electric field in the same direction as holes with positive charge and positive mass.
• Thus, the charge transport in the valence band can be fully accounted for by considering hole motion alone.
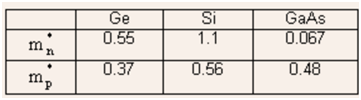
• The electron and hole effective masses are denoted by m^*_n and m^*_p  respectively.

Table: the effective mass for electrons and holes (Χ m₀, where m₀ is the rest mass for electrons)