An office contains two envelope stuffing machines. Machine A can stuff a batch of envelopes within 5 hours, whereas Machine B can stuff batch of envelopes within 3 hours. How much time it take the two machines working together to stuff a batch of envelopes?

Solution

Let t is the time that it takes both of machines, working together, to stuff batch of envelopes. The word equation for problem is following,

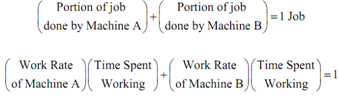
However we know that the time spent working is t we don't know about the work rate of each machine. In order to get these we'll have to use the initial information given about how much time it takes each machine to do the job independently.  We can employ the following equation to get these rates.

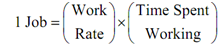
Let's begin with Machine A.

1 Job= ( Work Rate of A ) × (5) ⇒     Work Rate of A = 1/5

Now, Machine B.

1 Job = ( Work Rate of B) × (3)   ⇒   Work Rate of B = 1/3

Plugging these quantities in the main equation gives the following equation which we have to solve.

1/5 t +1/3 t = 1                                    Multiplying by 15 through both sides

3t + 5t = 15

8t = 15

t = 15/8 = 1.875 hours

Thus, it looks as it will take two machines, working together, 1.875 hours to stuff batch of envelopes.