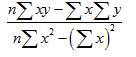Example of Regression Equation
An investment company advertised the sale of pieces of land at different prices. The given table shows the pieces of land their costs and acreage
|
Piece of land
|
(x)Acreage Hectares
|
(y) Cost £ 000
|
xy
|
x2
|
|
A
|
2.3
|
230
|
529
|
5.29
|
|
B
|
1.7
|
150
|
255
|
2.89
|
|
C
|
4.2
|
450
|
1890
|
17.64
|
|
D
|
3.3
|
310
|
1023
|
10.89
|
|
E
|
5.2
|
550
|
2860
|
27.04
|
|
F
|
6.0
|
590
|
3540
|
36
|
|
G
|
7.3
|
740
|
5402
|
53.29
|
|
H
|
8.4
|
850
|
7140
|
70.56
|
|
J
|
5.6
|
530
|
2969
|
31.36
|
|
|
Σx =44.0
|
Σy = 4400
|
Σxy= 25607
|
Σx2 = 254.96
|
Required
Find out the regression equations of
i. y on x and thus estimate the cost of a piece of land along with 4.5 hectares
ii. Estimate the expected average if the piece of land costs of £ 900,000
Σy = an + bΣxy
Σxy = a∑x + bΣx2
By substituting of the suitable values in the above equations we have
4400 = 9a + 44b ........ (i)
25607 = 44a + 254.96b ........(ii)
By using multiplying equation .... (i) by 44 and equation ...... (ii) by 9 we have
193600 = 396a + 1936b ........ (iii)
230463 = 396a + 2294.64b ........(iv)
By using subtraction of equation .... (iii) from equation ...... (iv) We have
36863 = 358.64b
102.78 = b
by substituting for b in equation........ (i)
4400 = 9a + 44( 102.78)
4400 - 4522.32 = 9a
-122.32 = 9a
-13.59 = a
Hence the equation of the regression line of y on x is
Y = 13.59 + 102.78x
When the acreage or hectares is 4.5 then the cost
(y) = -13.59 + (102.78 x 4.5)
= 448.92
= £ 448, 920
Note that
Where the regression equation is described by
y= a + bx
Whereas a is the intercept on the y axis and
b is the slope of the line or else regression coefficient
n is the sample size
After that,
intercept a = (Σy - bΣx)/n
Slope b =