Example of Prolog:

We can say that this is also true if there are four even numbers. Now we have our first rule:

• If there are three or four even numbered cards, such player one should choose the highest even numbered card in their first go probably.

Whenever there are three or four odd cards it's not difficult to see that the most rational action for player one is to choose the highest odd numbered card:

• If there are three or four odd numbered cards, such player one should choose the highest odd numbered card in their first go. The only other situation is when there are two even and two odd cards. However, this case, I'll leave it as an exercise to convince yourselves that there are no rules governing the choice of player one's first card: they can simply choose randomly, it means that they're not going to win unless player two makes a mistake.

Just to write an expert system to decide what type card to choose in a game, that we will require to translate our rules into first-order logic, then into a Prolog implementation. Now in our first rule states such in a game, eg:

There is the meaning of the predicates is as obvious as it seems. Correspondingly our second rule can be written like:

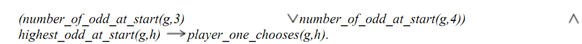
So there are many different ways to encode these rules as a Prolog program but different implementations will differ in their execution time. Just for our simple program, there it doesn't truly matter that predicates we choose to implement. If we will make our top level predicate as:

player_one_chooses/2.

Than the predicate will take a list of card numbers such the first argument, it will choose a member of this list to put as the second argument. In fact in this way, there the same predicate can be used in order to make second choices.