Examine the state of stress at the junction of flange:

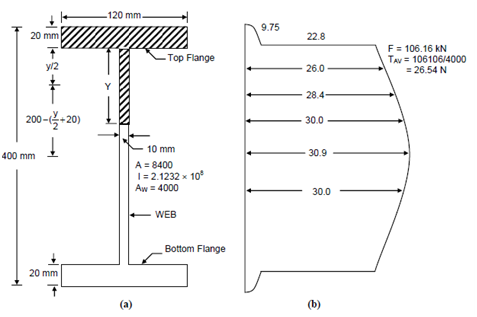
A beam of I-section as shown in Figure (a) is subjected to a bending moment of 84.928 kN m and a shear force of 106.1 kN. Examine the state of stress at the junction of flange and web.

Figure

Solution

(In this case also the solution will be provided by stating the expressions for stress components, without their derivation which will be dealt with in addition.)

A neutral axis of the section will be the horizontal axis through the centroid of the section.

The bending stress at a layer 'y' above the neutral axis is given as,

σ_x = -My/I                                                                    . . . (iv)

here, I is the moment of inertia of the section and M is the bending moment on the section.

The shear stress at some layer is given as

 τ_xy= Q . Ay¯/Ib                                                              . . . (v)

here, Ay¯  is the moment of the area of that portion of the section above or below the layer about the neutral axis, b is the breadth of the layer and Q, the shear force at the section.

For the cross-section given, the moment of inertia is given as 2.1232 × 10⁸ mm⁴. Total depth of beam = 400 mm.

∴ Neutral axis is at a depth of 200 mm from top.

A distance of the layer at junction of web and flange from the neutral axis is 180 mm.

Determination of Bending Stress

σ_x   = - My/I - 84.928 × 10⁶ × 180/2.1232 × 10⁸ = -72 N/mm²

Determination of Shear Stress

In this case Ay¯ will be given by the moment of the flange area about the neutral axis.

Ay¯ = 120 × 20 × (180 + 20/2)= 4.56 × 10⁵  mm³

τ_xy = 106.1× 10³ ×4.56 ×10⁵/2.1232× 10⁸×10 = 22.8 N/mm²

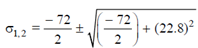
Thus, we get,

σ₁  = 6.613 N/mm²

σ₂  = - 78.613 N/mm²

τ_max  = 42.613 N/mm²

You may obverse here in which the junction among flange and web will become the critical zone, while the shear force at the section is considerable. Therefore, experience will tell you, while to look for critical zones in various cases.