Evaluate the centroid of an area:

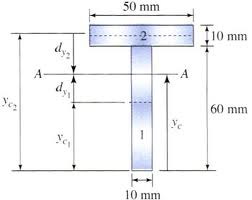
Determine the centroid of an area shown in Figure (a).

Solution

This problem may be attempted in two ways as illustrated in Figures (b) and  (c). The total area A is divided in three parts A₁, A₂ and A₃ in Figure (b), whereas the same area A may be divided in two parts A₁′ and (-) A₂′(shown shaded) in Figure (c).

Consider G be the centroid of area A as illustrated in Figure with (x, y) co-ordinates, with respect to axes OX and OY.

Table

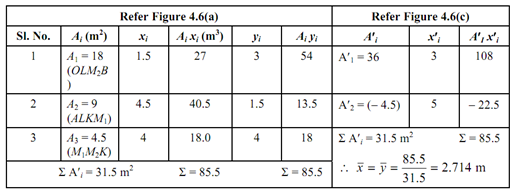
∴ x = 85.5/31.5                                           y = 85.5/ 31.5;

   x = 2.714 m,                                             y = 2.714 m

This is to be noted down from the above Table that whichever way we let the division of regular area, either all of the positive or some of them negative, we must finally get the unique value of

1.      ∑ A_i ,

2.      ∑ A_i  x_i , and

3.      ∑ A_i  y_i .

For a given area A, the co-ordinates, x and y , shall therefore, be a unique value.

Note :  If the problem of C. G. (Centre of gravity) of a uniform plate is let where out of a square plate OACB a triangular part M₁ C M₂ is cut out, the location of centre of gravity of such a plate is the similar as position of centroid of area in Figure).