This question explores the effect of estimation error on apparent arbitrage opportunities in a controlled simulation setting. We simulate returns for N = 10 assets over T = 30 years. We will use the first 20 years for estimation and the selection of the hedge portfolio ("in-sample"), and the remaining 10 years as "out-of-sample" performance evaluation period. Start out with a market return R_M that is normally distributed with mean μ_M = 0:05 and standard deviation σ_M = 0:15, and assume a risk-free rate R_f = 0. All assets follow the factor model R_n,t = α_n + β_nR_M,t + ε_n,t, where we assume n = 1 for all n.

We will consider three sets of parameters for the return generating process.

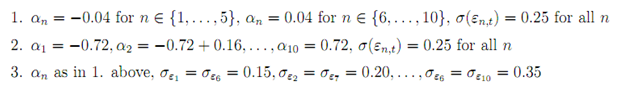
For each parameterization, perform 100 simulations (data table) for returns on market-neutral zero-investment portfolios and report the average holding period mean return and how often you investment loses money over the performance evaluation period assuming that

i) You know the parameters of the return generating process and invest equal amounts in every stock with positive alpha and short equal amounts of every stock with negative alpha

ii) You estimate the parameters and invest $1 in the stock with the highest alpha (if there is one), and short $1 of the stock with the most negative alpha (if there is one)

iii) You estimate the parameters and invest equal amounts in every stock with positive alphas (if there are) and short equal amounts of every stock with negative alphas (if there are)

iv) You estimate the parameters and come up with a more sophisticated investment strategy. Compare and explain your findings.

Notes

• Start out with fewer simulations in your data table until you are con dent everything works
• Your investment should hedge out all market risk (using your best estimates)
• Take great care programming the portfolio weights in (ii)-(iv). If everything is done right, changing parameters and running the simulations should not take much time.