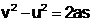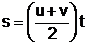Given a particle moving along a straight line with fixed acceleration a. Let u be the initial velocity of the particle and v be the velocity at time t. So by definition,

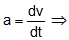                                                                                             dv = a dt

                        Integrating,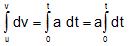 

(a being a constant may be taken out of the integral)                 v - u = at

                                           v = u + at                                                                     ...(i)

Further, 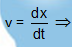            dx = vdt

But,      v = u + at,               dx = (u + at)dt

Integrating within limits, equations change into,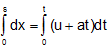                 

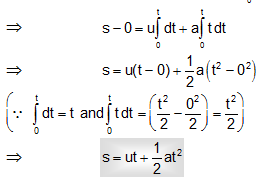
                                                                                                          ...(ii)

Again, going back to definition of acceleration, we have,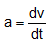    

Multiply and divide RHS of above equation by dx, equation gets,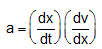    

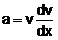                                            adv = adx

Integrating within limits, equation converts,                  →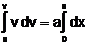       

      →          

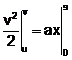
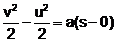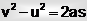
                                                                       ...(iii)

From (i) and (iii) we also result that, 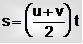                                         ...(iv)

Equation (iv) is a special equation, as we do not have a in this equation, but still it belongs to motion, which is uniformly accelerated.

To result, we again write the equation of motion for constant acceleration below.

v = u + at ;     s = ut + 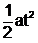;