Steps uses in the Cohen Sutherland Line Clipping Algorithm are:

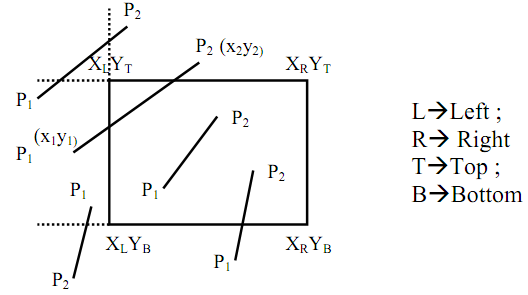
Figure: Steps for Cohen Sutherland Line Clipping

STEP 1:

Input:

 x_L , x_R , y_T , y_B , P₁ ( x₁ , y₁ ), P₂ ( x₂ , y₂ )

 Initialize i = 1

While i <= 2

if x_i  < x_L  then bit 1 of code -P_i = 1 else 0

 if x_i > x_R then bit 2 of code -P_i =1 else 0         

: The endpoint codes of the line are then set

 if  y_i  < y_B then bit 3 of code -P_i = 1 else 0

if  y_i  > y_T then bit 4 of code -P_i = 1 else 0

i = i +1

end while

 i = 1

STEP 2:

Initialize j = 1

While j <= 2

 if x_j   < x_L then C_j left = 1 else C_j left = 0

 if x j > x R   then C j right = 1 else C j right   = 0

 : Set flags as per to the position of the line endpoints with respect to window

if  y_j  < y_B   then C_j bottom  = 1 else C_j bottom  = 0 edges

if  y _j  > y_T then C_j top = 1 else C _jtop  = 0

 end while

STEP 3: If codes of P1and P2 are both equivalent to zero then draw P₁P₂ are wholly visible

STEP 4: If logical intersection or AND operation of code -P₁ and code -P₂ is not equivalent to zero then avoid P₁P₂ are wholly invisible

STEP 5: If code -P₁= 0 then swap P₁ and P₂ with their flags and also set i = 1

STEP 6: If code -P₁ < > 0 then

for i = 1,

{if C_{1 left} = 1 then

find intersection ( x_L , y'_L )

assign code to ( x_L , y'_L )

P1 = ( x_L , y'_L )

end if

i = i + 1;

go to 3

}

with left edge vide eqn. (C)

 for i = 2,

{if C_{1 right} = 1 then

find intersection ( x_R , y'_R ) with right edge vide eqn. (D)

assign code to ( x_R , y'_R )

P₁ = ( x_R , y'_R )

end if

i = i + 1 go to 3

}

for i = 3

{if C1 bottom = 1 then

find intersection ( x '_B , y_B ) with bottom edge vide eqn. (B)

assign code to ( x '_B , y_B )

P1 = ( x '_B , y_B )

end if

i = i + 1 go to 3

}

for i = 4,

{if C_{1 top} = 1 then

find intersection ( x '_T , y_T ) vide eqn. (A) with top edge assign code to ( x '_T , y_T )

P₁ = ( x '_T , y_T )

end if

i = i + 1 go to 3

}

end