Determine the slope following lines.  Sketch the graph of line.

      The line which contains the two points (-2, -3) and (3, 1) .  

Solution

we'll need to do is employ the slope formula to determine the slope & then plot the two points & connect them along a line to get the graph.

The line which contains the two points ( -2, -3) and (3,1) .

Do not worry which point gets the subscript of 1 & which subscript of 2. Either way will get the similar answer. Usually, we'll just take them into the order listed.  Thus, here is the slope for this part.

                           m =1 - (-3)/ 3 - (-2) = 1+3 /3+2 = 4/5

Be careful with minus signs in these computations.  This is easy to lose track of them.  Also, while the slope is a fraction, as it is here, leave it like a fraction.  Do not change to a decimal unless you absolutely need to.

Following is a sketch of the line.

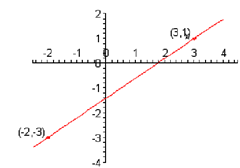
Notice that this line enhance as we move from left to right.