Determine the point of contraflexure:

Draw the shear force & bending moment diagram for 10 m span overhanging beam along overhanging part of 4 m subjected to a system of loads as illustrated in Figure . Determine the maximum bending moment and also situated the point of contraflexure.

Solution

Taking moments around A and equating it to zero,

R _B   × 6 - (8 × 10) - 3 × 4 × ( 6 + (4/2)   - (20 × 4) - (10 × 2) = 0

R_B = 46 kN

R_A = 10 + 20 + (3 × 4) + 8 - R_B = 50 - 46 = 4 kN

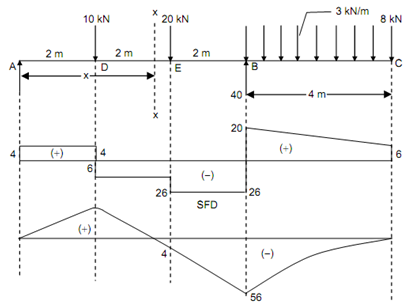
Figure

Shear Force (beginning from the end A)

SF at A, F_A = + 4 kN

SF just left of D, F_D = + 4 kN

SF just right of D, F_D = + 4 - 10 = - 6 kN

 SF just left of E, F_E = - 6 kN

SF just right of E, F_E = - 6 - 20 = - 26 kN

 SF just left of B, F_B = - 26 kN

SF just right of B, F_B = - 26 + 46 = + 20 kN

SF just left of C, F_C = + 20 kN = Load at C

Bending Moment

BM at C, M_C  = 0

BM at B, M _A= (0.3 × 10) - (1 × 10 × (10/2) )  = - 47 kN m

BM at E, M_E = + (4 × 4) - (10 × 2) = - 4 kN m

BM at D, M_D = + (4 × 2) = + 8 kN m

Maximum Bending Moment

As SF changes sign at D & B, the maximum positive bending moment shall occur at D and maximum -ve bending moment shall take place at B.

M_max (positive) = + 8 kN m

M_max (negative) = - 56 kN m

Point of Contraflexure

BM changes sign among D & E. Thus, consider a section XX at distance x from the end A.

BM at section XX,

M_x = + 4 x - 10 (x - 2)

 Equating this to zero, we obtain

4 x - 10 (x - 2) = 0

4 x - 10x + 20 = 0

- 6x + 20 = 0

∴          x = 3.333 m

The point of contraflexure is at any distance of 3.333 m from the left end of A.