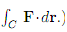Question 1. Use cylindrical coordinates to nd the mass of the solid of density e^z which lies in the closed region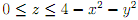 

Question 2. The density of a hemisphere of radius a (y  0) with its base centred at the origin is given by (x; y; z) =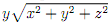

 Determine the mass of the hemisphere. Note that sphere is not in the upper half space z > 0.

Hint: The identity cos(2θ) = cos²θ  - sin²θ may be useful.

Question 3. Determine whether or not the vector eld F(x; y; z) = 14xyi + (7x²+ 18yz)j + 9y²k is conservative. If it is conservative, nd a function f(x; y; z) such that

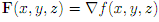
Question 4. Evaluate the line integral

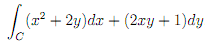
where C is the curve from (0; 0) to (0; 2) consisting of the path from (0; 0) to (1; 1) along the parabola y = x² , followed by the path along straight line from (1; 1) to (0; 2).

Question 5. A particle starts at the point (-4,0), moves along the x-axis to (0,0) and the y-axis to (0,4) and then along the arc y =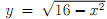 to the starting point. Use Green's theorem to nd the work done on this particle by the force eld F(x; y) = (18x; 6x³
+ 18xy² ).

(Hint: Work done by a force eld F along a curve C is given by the line integral