Q. (a) Determine the'effective  focal length' of the grouping of the two lenses in Exercise 9.10 if they are placed 8.0 cm a part with their principal axes  coincident. Performed the answer depend on which side of the combination a beam of parallel light is incident? Is the idea of effective focal length of this system useful at all? (b)T he object 1.5 cm in size is placed on the side of the convex lens in the arrangement (a) above. The distance among the object and the convex lens is 40cm.  Determine the exaggeration produced by the two < lens system and the size of the image.

Answer

A Focal length of the convex lens, f1=30cm

A Focal length of the concave lens, f2=-20cm

The Distance between the two lenses d=8.0cm

(a)While the parallel beam of light is incident on the convex lens first:

As-per to the lens formula we have

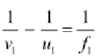
Where

U₁=Object distance=∞

v₁=Image distance

v₂=Image distance

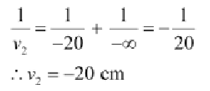
The image will perform as a real object for the convex lens.

Pertaining lens formula to the convex lens, we have:

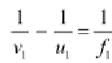
Where,

U₁=Object distance

=- (20+d)=-(20+8)=-28cm

V₁=Image distance

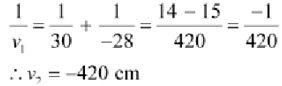
Therefore the parallel incident beam appears to diverge from a point that is (420-4) 416 cm from the left of the centre of the combination of the two lenses.

The answer does depend on the side of the combination at which the parallel beam of light is incident. The notion of effectual focal length does not seem to be useful for this combination.

(b)Height of the image h 1=1.5cm

An Object distance from the side of the convex lens u₁=-40cm

|u₁|=40cm

As-per to the lens formula:

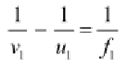
Where v₁=Image distance

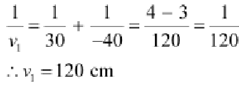
Magnification=120/40=3

Therefore the magnification due to the  convex lensis3.

The image produced by the convex lens acts as an object for the concave lens .According to the lens formula:

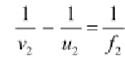
Where

U₂=Object distance

=+ (120-8)=112cm.

V₂ =Image distance

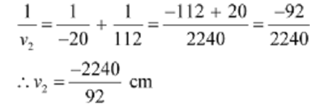
Magnification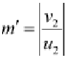

= 2240/92 x 1/112  = 20/92

Therefore the magnification due to the concave lens is 20/92.

The magnification produced by the grouping of the two lenses is calculated as

m x m'

= 3 x 20/92 = 60/92  = 0.652

The magnification of the grouping is given as

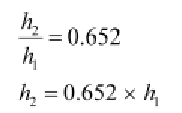
Where

h₁= Object size=1.5cm

h₂ = Size of the image

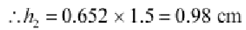
Therefore the height of the image is 0.98 cm.