Determine the deflection at free end:

For the beam illustrated in Figure, determine the deflection at free end and the maximum deflection.

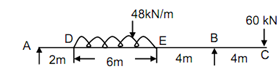
Figure

Solution

R_A + R_B  = 48 × 6 + 60 = 348 kN         ----------- (1)

Σ M about A = 0.

48 × 6 × (2 + 3) + 60 × 16 = R_B  × 12

 ∴         R_B  = 200 kN (↑)                        ---------- (2)

From Eqs. (1) and (2),

R_A  = 148 kN (↑)                         ------ (3)

Apply the Udl in downward and upward directions in the portion EC

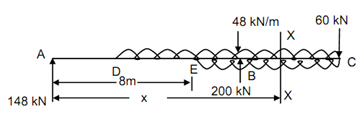
Figure

M = 148 x - (48/2) [ x - 2] [ x - 2] + (48/2) [ x - 8] [ x - 8] + 200 [ x - 12]

= 148 x - 24 [ x - 2]²  + 24 [ x - 8]²  + 200 [ x - 12] ----------. (4)

EI d ² y/ dx²      = M = 148 x - 24 [ x - 2]²  + 24 [ x - 8]²  + 200 [ x - 12]          -------- (5)

EI (dy/ dx )= 74 x² - 8 [ x - 2]³ + 8 [ x - 8]² + 100 [ x - 12] ²+ C₁          ------- (6)

EIy (74/3) x³  - 2 [ x - 2]⁴  + 2 [ x - 8]⁴  + 100 [ x - 12]³ + C1 x + C₂   ---------- (7)

The boundary conditions are :

At A,       x = 0,           y = 0                 ------- (8)

At B,          x = 12 m,        y = 0                 ------- (9)

From Eqs. (7) and (8),

C₂ = 0   ------------- (10)

From Eqs. (7) and (9),

0 = (74 /3)× 12³ - 2 [12 - 2]⁴  + 2 [12 - 8]⁴  + C₁ × 12

∴          C₁ = - 1928                              ------------ (11)

∴          EIy = 74 x³  - 2 [ x - 2]⁴  + 2 [ x - 8]⁴  + 100 [ x - 12]³  - 1928 x

Deflection at free end, x = 16 m

EIy C   = (74 /3)× 16³  - 2 [16 - 2]⁴  + 2 [16 - 8]⁴  + 100 [16 - 12]³  - 1928 × 16 = 3680

∴          y_C  =+  3680 / EI

Maximum Deflection : It occurs between D and E.

dy / dx = 0

0 = 74 x²  - 8 [ x - 2]³  - 1928

= 74 x²  - 8 x³  + 64 + 48 x²  - 96 x - 1928

= 8 x³  - 122 x²  + 96 x + 1928

By trial and error, x = 5.7 m

EIy _max     = 74 × 5.7³  - 2 [5.7 - 2]⁴  - 1928 × 5.7 = - 6796.3

∴          y_max = - 6796.3 / EI