Determine reactions at supports of loaded beam:

Determine reactions at supports A and B of loaded beam as shown in the figure given below. 

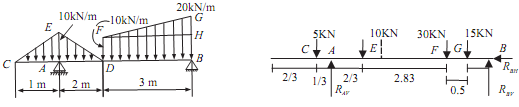
Sol.: First consider the free body diagram of the figure give to us. In which ?CEA, AED and

FHG shows point load and rectangle FHDB shows point load.

Point load of ?CEA = 1/2 × AC × AE = 1/2 × 1 × 10 = 5KN, act at a distance 1/3 of AC (that is, 0.333m) from point A

Point load of ?AED = 1/2 × AD × AE = 1/2 × 2 × 10 = 10KN

act at a distance 1/3 of AD (that is, 0.666m )from point A

Now divided the diagram DBGF in to two parts A ?FHG and a rectangle FHDB. Point load of Triangle FHG = 1/2 × FH × HG = 1/2 × 3 × (20 - 10) = 15KN

act at distance 1/3 of FH (that is, 1.0m )from point H

Point load of Rectangle FHDB = DB × BH = 3 × 10 = 30KN

act at a distance 1/2 of DB (that is, 1.5m )from point D

At Point A roller support that is, only vertical reaction (RAV), and point B hinged support that is, a horizontal reaction (RBH) and a vertical reaction (RBV). All point load are shown in the given figure

∑H = 0;

R_BH   = 0

R_BH = 0                                                              .......ANS

∑V  = 0;

R_AV  + R_BV  - 5 - 10 - 30 - 15 = 0

R_AV  + R_BV = 60KN                                                                                                                              ...(i)

Now taking moment about 'A'

- 5 × 1/3 + 10 × 0.66 + 30 × 3.5 + 15 × 4 - RBV  × 5  = 0

R_BV = 34 KN                                                   .......ANS

Putting the value of RDV in the equation (1)

R_AV = 26KN                                                     .......ANS